How to Read Arellano-bond Estimator Output Stata
Gild STATA
Dynamic panel-data (DPD) analysis
Stata has suite of tools for dynamic console-data analysis:
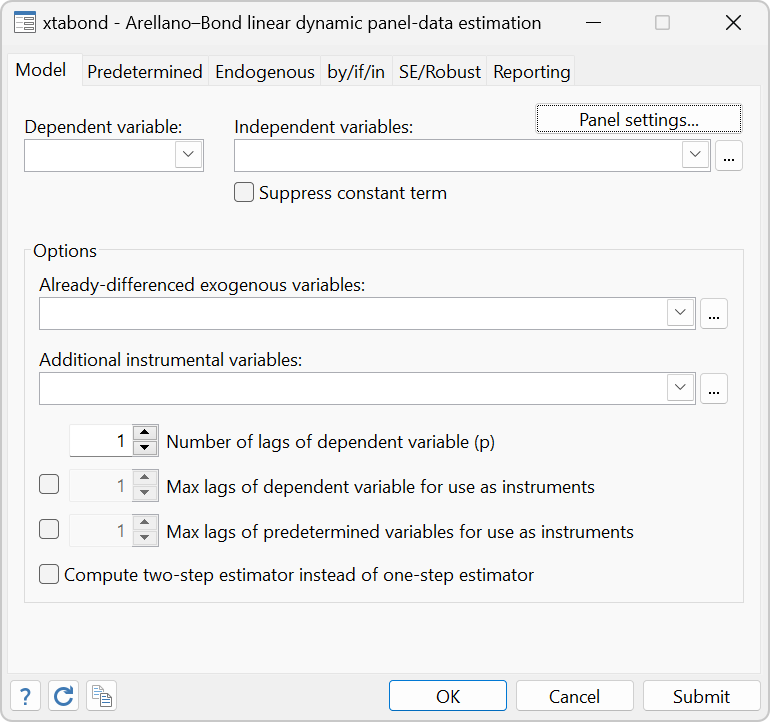
- xtabond implements the Arellano and Bond estimator, which uses moment weather condition in which lags of the dependent variable and offset differences of the exogenous variables are instruments for the showtime-differenced equation.
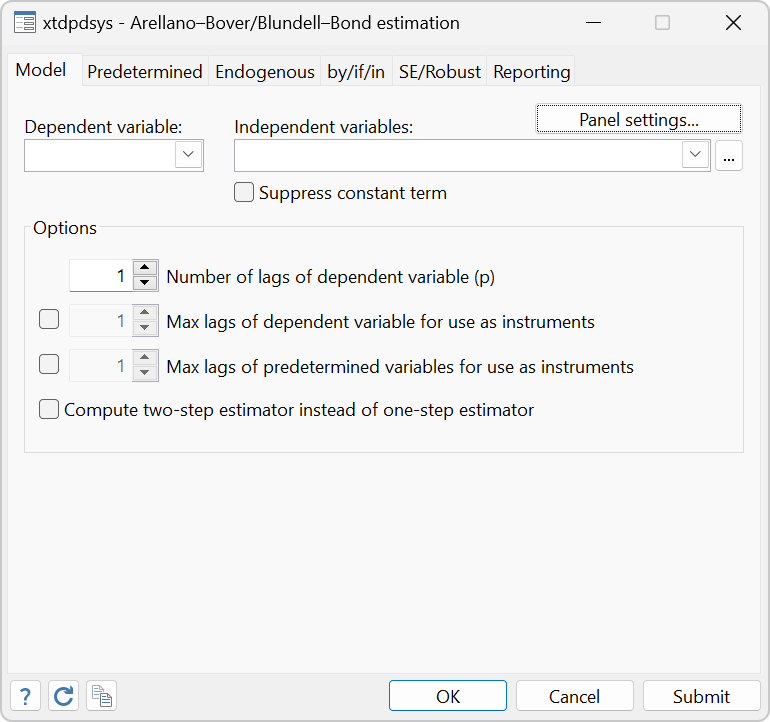
- xtdpdsys implements the Arellano and Bover/Blundell and Bond system estimator, which uses the xtabond moment conditions and moment conditions in which lagged first differences of the dependent variable are instruments for the level equation.
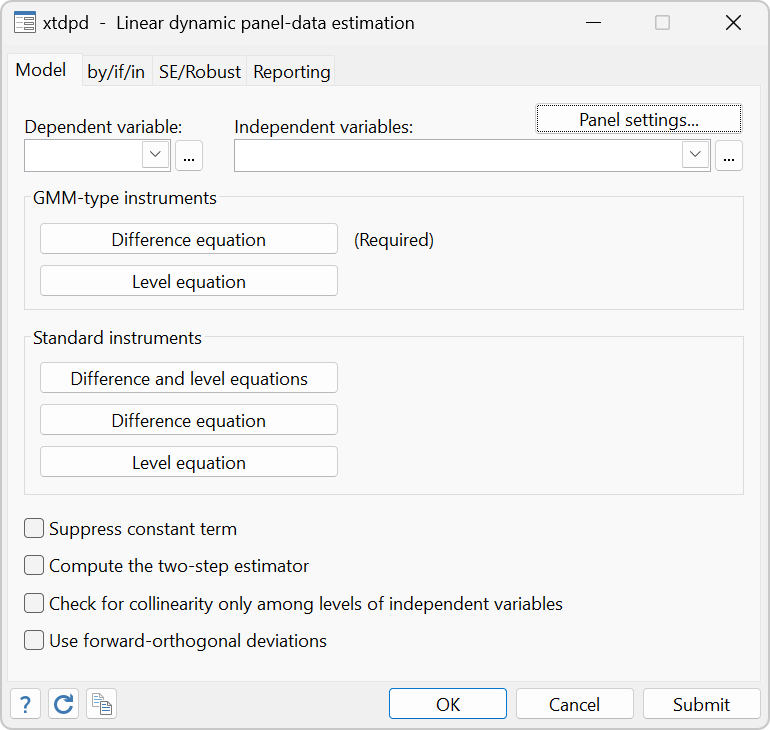
- xtdpd, for advanced users, is a more flexible alternative that tin fit models with low-order moving-average correlations in the idiosyncratic errors and predetermined variables with a more complicated structure than allowed with xtabond and xtdpdsys.
- Postestimation tools allow you to exam for serial correlation in the first-differenced residuals and test the validity of the overidentifying restrictions.
Example
Edifice on the work of Layard and Nickell (1986), Arellano and Bond (1991) fit a dynamic model of labor need to an unbalanced panel of firms located in the United Kingdom. Get-go nosotros model employment on wages, uppercase stock, industry output, year dummies, and a time tendency, including one lag of employment and two lags of wages and upper-case letter stock. Nosotros will use the i-pace Arellano–Bond reckoner and request their robust VCE:
. webuse abdata . xtabond north Fifty(0/2).(w k) yr1980-yr1984 year, vce(robust) Arellano–Bond dynamic panel-data estimation Number of obs = 611 Group variable: id Number of groups = 140 Fourth dimension variable: yr Obs per group: min = four avg = 4.364286 max = half dozen Number of instruments = twoscore Wald chi2(13) = 1318.68 Prob > chi2 = 0.0000 Ane-pace results (Std. err. adapted for clustering on id)
| Robust | ||||||||
| n | Coefficient std. err. z P>|z| [95% conf. interval] | |||||||
| northward | ||||||||
| L1. | .6286618 .1161942 v.41 0.000 .4009254 .8563983 | |||||||
| west | ||||||||
| --. | -.5104249 .1904292 -ii.68 0.007 -.8836592 -.1371906 | |||||||
| L1. | .2891446 .140946 2.05 0.040 .0128954 .5653937 | |||||||
| L2. | -.0443653 .0768135 -0.58 0.564 -.194917 .1061865 | |||||||
| 1000 | ||||||||
| --. | .3556923 .0603274 v.90 0.000 .2374528 .4739318 | |||||||
| L1. | -.0457102 .0699732 -0.65 0.514 -.1828552 .0914348 | |||||||
| L2. | -.0619721 .0328589 -1.89 0.059 -.1263743 .0024301 | |||||||
| yr1980 | -.0282422 .0166363 -1.70 0.090 -.0608488 .0043643 | |||||||
| yr1981 | -.0694052 .028961 -2.40 0.017 -.1261677 -.0126426 | |||||||
| yr1982 | -.0523678 .0423433 -1.24 0.216 -.1353591 .0306235 | |||||||
| yr1983 | -.0256599 .0533747 -0.48 0.631 -.1302723 .0789525 | |||||||
| yr1984 | -.0093229 .0696241 -0.thirteen 0.893 -.1457837 .1271379 | |||||||
| year | .0019575 .0119481 0.16 0.870 -.0214604 .0253754 | |||||||
| _cons | -2.543221 23.97919 -0.11 0.916 -49.54158 44.45514 | |||||||
Because nosotros included one lag of northward in our regression model, xtabond used lags 2 and dorsum every bit instruments. Differences of the exogenous variables also serve as instruments.
Here we refit our model, using xtdpdsys instead so that we can obtain the Arellano–Bover/Blundell–Bond estimates:
. xtdpdsys due north L(0/2).(west thou) yr1980-yr1984 year, vce(robust) Arrangement dynamic panel-information estimation Number of obs = 751 Group variable: id Number of groups = 140 Time variable: year Obs per group: min = 5 avg = 5.364286 max = 7 Number of instruments = 47 Wald chi2(13) = 2579.96 Prob > chi2 = 0.0000 One-step results
| Robust | |||||||
| n | Coefficient std. err. z P>|z| [95% conf. interval] | ||||||
| n | |||||||
| L1. | .8221535 .093387 eight.eighty 0.000 .6391184 1.005189 | ||||||
| w | |||||||
| --. | -.5427935 .1881721 -ii.88 0.004 -.911604 -.1739831 | ||||||
| L1. | .3703602 .1656364 2.24 0.025 .0457189 .6950015 | ||||||
| L2. | -.0726314 .0907148 -0.fourscore 0.423 -.2504292 .1051664 | ||||||
| k | |||||||
| --. | .3638069 .0657524 v.53 0.000 .2349346 .4926792 | ||||||
| L1. | -.1222996 .0701521 -1.74 0.081 -.2597951 .015196 | ||||||
| L2. | -.0901355 .0344142 -2.62 0.009 -.1575862 -.0226849 | ||||||
| yr1980 | -.0308622 .016946 -1.82 0.069 -.0640757 .0023512 | ||||||
| yr1981 | -.0718417 .0293223 -ii.45 0.014 -.1293123 -.014371 | ||||||
| yr1982 | -.0384806 .0373631 -1.03 0.303 -.1117111 .0347498 | ||||||
| yr1983 | -.0121768 .0498519 -0.24 0.807 -.1098847 .0855311 | ||||||
| yr1984 | -.0050903 .0655011 -0.08 0.938 -.1334701 .1232895 | ||||||
| year | .0058631 .0119867 0.49 0.625 -.0176304 .0293566 | ||||||
| _cons | -10.59198 23.92087 -0.44 0.658 -57.47602 36.29207 | ||||||
Comparing the footers of the 2 commands' output illustrates the cardinal divergence between the 2 estimators. xtdpdsys included the lagged differences of northward every bit instruments in the level equation; xtabond did not.
The moment conditions of these GMM estimators are valid only if at that place is no series correlation in the idiosyncratic errors. Because the outset departure of white noise is necessarily autocorrelated, we need but concern ourselves with 2d and higher autocorrelation. Nosotros can employ estat abond to exam for autocorrelation:
. estat abond, artests(4) Dynamic panel-data estimation Number of obs = 751 Group variable: id Number of groups = 140 Time variable: year Obs per group: min = 5 avg = five.364286 max = 7 Number of instruments = 47 Wald chi2(13) = 2579.96 Prob > chi2 = 0.0000 Ane-step results (Std. err. adjusted for clustering on id)
| Robust | ||||||
| north | Coefficient std. err. z P>|z| [95% conf. interval] | |||||
| due north | ||||||
| L1. | .8221535 .093387 8.80 0.000 .6391184 1.005189 | |||||
| w | ||||||
| --. | -.5427935 .1881721 -ii.88 0.004 -.911604 -.1739831 | |||||
| L1. | .3703602 .1656364 2.24 0.025 .0457189 .6950015 | |||||
| L2. | -.0726314 .0907148 -0.80 0.423 -.2504292 .1051664 | |||||
| k | ||||||
| --. | .3638069 .0657524 five.53 0.000 .2349346 .4926792 | |||||
| L1. | -.1222996 .0701521 -i.74 0.081 -.2597951 .015196 | |||||
| L2. | -.0901355 .0344142 -2.62 0.009 -.1575862 -.0226849 | |||||
| yr1980 | -.0308622 .016946 -i.82 0.069 -.0640757 .0023512 | |||||
| yr1981 | -.0718417 .0293223 -2.45 0.014 -.1293123 -.014371 | |||||
| yr1982 | -.0384806 .0373631 -1.03 0.303 -.1117111 .0347498 | |||||
| yr1983 | -.0121768 .0498519 -0.24 0.807 -.1098847 .0855311 | |||||
| yr1984 | -.0050903 .0655011 -0.08 0.938 -.1334701 .1232895 | |||||
| year | .0058631 .0119867 0.49 0.625 -.0176304 .0293566 | |||||
| _cons | -x.59198 23.92087 -0.44 0.658 -57.47602 36.29207 | |||||
| Society z Prob > z | ||
| i -4.6414 0.0000 | ||
| 2 -1.0572 0.2904 | ||
| 3 -.19492 0.8455 | ||
| 4 .04472 0.9643 | ||
References
- Arellano, Yard., and S. Bond. 1991.
- Some tests of specification for panel information: Monte Carlo bear witness and an awarding to employment equations. The Review of Econometric Studies 58: 277–297.
- Layard, R., and Due south. J. Nickell. 1986.
- Unemployment in Britain. Economica 53: 5121–5169.
Explore more time-series features in Stata.
rogerthemaged1950.blogspot.com
Source: https://www.stata.com/features/overview/dynamic-panel-data/
Publicar un comentario for "How to Read Arellano-bond Estimator Output Stata"